Metrics

Metrics#

There are a lot of goodness of fit metrics and ways to characterize loss.

Basics#

  • A model fits the data well when the differences between the observed values and predicted values are small and unbiased

  • the differences between the observed values and predicted values are called residuals

  • as the goodness of fit increases, the model is better fitted to the data

Regression Metrics#

  • Common Terms

    • \(y\) = observed values

    • \(y_i\) = observed value \(i\)

    • \(\hat y_i\) = predicted value \(i\)

    • \(\bar y_i\) = average of the observed values \(i\)

    • \(n\) = sample size

  • R-squared (also known as Coefficient of Determination) is the ratio of the variance that’s explained by the model to the variance that’s explained by a simple mean. It’s usually \(0-1\), though it can be negative if the model is worse at explaining variance than just guessing the mean regardless of inputs. \(R^2\) always increases as more independent variables are added, whether or not those variables are useful predictors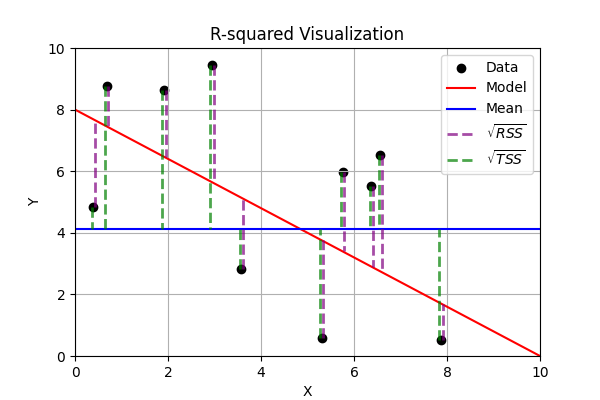 Pic R2 – Score: Higher values indicate better fit ranging from 0 to 1.

    • \(R^2=1-\Large\frac{RSS}{TSS}=1-\Large\frac{\sum_{i=1}^n(y_i-\hat y_i)^2}{\sum_{i=1}^n(y_i-\bar y_i)^2}\)

      • \(RSS\) = Residual Sum of Squares = \(\sum_{i=1}^n(y_i-\hat y_i)^2\)

      • \(TSS\) = Total Sum of Squares = \(\sum_{i=1}^n(y_i-\bar y_i)^2\)

  • Adjusted R-squared is a modification of R-squared that penalizes the inclusion of variables that don’t actually contribute to prediction

    • \(\bar R^2=1-\Large\frac{RSS/DOF_{res}}{TSS/DOF_{tot}}\) \(= 1-(1-R^2)\Large\frac{n-1}{n-p-1}\)

      • \(DOF_{res}\) = Degrees of Freedom of population variance around mean

      • \(DOF_{tot}\) = Degrees of Freedom of population variance around model

      • \(p\) = total number of explanatory variables (inputs)

  • MAE = Mean Absolute Error - same scale as target variable, robust to outliers, difficult to take derivatives of due to absolute value

    • \(MAE = \frac{1}{n} \sum_{i=1}^n|y_i-\hat{y}_i|\)

  • NMAE = Normalized Mean Absolute Error - normalizes the absolute error by the range of actual values, making it a relative relative metric

    • \(NMAE = \Large\frac{\frac{1}{n}\sum_{i=1}^n{|\hat{y}_i-y_i|}}{\frac{1}{n}\sum_{i=1}^n{|y_i|}} = \frac{MAE(y,\hat{y})}{mean(|y|)}\)

  • MSE = Mean Squared Error - vulnerable to outliers because the error is squared

    • \(MSE =\frac{1}{n}\sum_{i=1}^n (\hat{y}_i - y_i)^2\)

  • Huber Loss: A hybrid loss function that transitions from MAE to MSE for larger errors, providing balance between MAE’s robustness and MSE’s sensitivity to outliers.

    • \(L_\delta = \begin{cases}\frac{1}{2}(y-\hat{y})^2 &|y-\hat{y}|<\delta \\ \delta((y-\hat{y})-\frac{1}{2}\delta) & |y-\hat{y}|\ge\delta\end{cases}\)

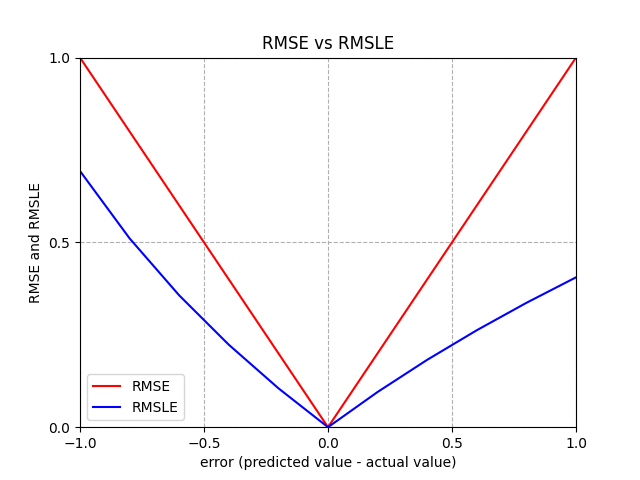
  • RMSE = Root Mean Squared Error - same training results as using MSE, still vulnerable to outliers, compare with MAE to see prevalence of outliers

    • \(RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^n (\hat{y}_i - y_i)^2}\)

  • RMSLE = Root Mean Squared Log Error - logs make it relative metric (ignore scale of data), less vulnerable to outliers than \(RMSE\), asymmetric (larger penalty if \(\hat{y}_i < y_i\) than if \(\hat{y}_i > y_i\))

    • \(RMSLE = \sqrt{\frac{1}{n}\sum_{i=1}^n (\ln{(\hat{y}_i+1)} - \ln{(y_i+1)})^2} =\Large\sqrt{\frac{1}{n}\sum_{i=1}^n (\ln{\frac{\hat{y}_i+1}{y_i+1}})^2}\)

    • RMSE vs RMSLE

  • MAPE = Mean Absolute Percentage Error (AVOID LIKE THE PLAGUE) fails if any \(y_i=0\), higher penalty for small \(y_i\), higher penalty for \(\hat{y}_i > y_i\) than \(\hat{y}_i < y_i\)

    • \(MAPE = \Large\frac{1}{n}\sum_{i=1}^{n}{|\frac{y_i-\hat{y}_i}{y_i}|}*100\)

  • SMAPE = Symmetric Mean Absolute Percentage Error (AVOID) improves somewhat on MAPE but still controversial, not symmetric, and the equation itself varies by source

    • \(SMAPE = \Large\frac{1}{n}\sum_{i=1}^{n}{\frac{|y_i-\hat{y}_i|}{y_i+\hat{y}_i}}\)

  • \(BIC\) = Bayesian Information Criterion evaluates goodness of fit \(-2\ln(L)\) while penalizing complexity to avoid overfitting \(k\ln(n)\)

    • \(BIC = -2\ln(L) + k\ln(n)\)

      • \(L\) = likelihood of the model given the data

      • \(k\) = number of parameters in the model

  • \(AIC\) = Akaike Information Criterion

    • \(AIC = 2k - 2 \ln(\hat L)\)

Metric

Penalizes Large Errors

Sensitive to Outliers

Interpretability

Recommended

MAE

✗

-

+++

✓

MSE

✓

+

+

✓

RMSE

✓

+

++

✓

MAPE

✗

Varies

++

✗

Classification Metrics#

  • Accuracy for Classifiers is a little different, and sometimes your priority changes

    • Sometimes it’s more important to catch everything, even if you catch some false positives

    • Sometimes it’s more important that you only catch stuff you’re sure about, and no false positives

  • Results

    • TP (True Positive): The model correctly predicted a positive outcome

    • TN (True Negative): The model correctly predicted a negative outcome

    • FP (False Positive): The model incorrectly predicted a positive outcome (Type I error)

    • FN (False Negative): The model incorrectly predicted a negative outcome (Type II error)

  • Can display with a Confusion Matrix

    • the link also explains the rest of these details and has example sklearn code to make Confusion Matrices

    • like this one for a model trying to classify emails as real or spam

    • (a real Confusion Matrix would put counts in each cell)

Predicted as Spam

Predicted as Real

Actually was Spam

TP (True Positive)

FN (False Negative)

Actually was Real

FP (False Positive)

TN (True Negative)

  • Metrics

    • Accuracy = how many predictions were correct out of the total predictions (can be misleading if one result is more dominant than another)

    • Precision = how many Positive Instances you caught (important if you can’t afford False Positives)

    • Recall = proportion of True Positives detected out of all Positive Instances (important if you can’t afford False Negatives)

    • F1-Score = combines Precision and Recall, assuming False Positives and False Negatives are equally important

    • Specificity = how good the model is at correctly identifying Negative Instances

    • Type 1 Error = error from False Positives

    • Type 2 Error = error from False Negatives

\[\begin{split} \begin{align} \text{Accuracy} &= \frac{TP + TN}{TP + TN + FP + FN} \\ \text{Precision} &= \frac{TP}{TP + FP} \\ \text{Recall} &= \frac{TP}{TP + FN} \\ \text{F1 Score} &= 2 \frac{\text{Precision} * \text{Recall}}{\text{Precision} + \text{Recall}} \\ \text{Specificity} &= \frac{TN}{TN + FP} \\ \text{Type 1 Error} &= \frac{FP}{FP + TN} \\ \text{Type 2 Error} &= \frac{FN}{TP + FN} \\ \end{align} \end{split}\]
Contents